Longest ZigZag Path in a Binary Tree

Leetcode Daily Challenge (19th April, 2023)

19 April, 2023

Contributors

Lakshit Chiranjiv Sagar

@lakshit-cs

Problem Statement:-

You are given the root of a binary tree.

A ZigZag path for a binary tree is defined as follow:

Choose any node in the binary tree and a direction (right or left).
If the current direction is right, move to the right child of the current node; otherwise, move to the left child.
Change the direction from right to left or from left to right.
Repeat the second and third steps until you can't move in the tree.

Zigzag length is defined as the number of nodes visited - 1. (A single node has a length of 0).

Return the longest ZigZag path contained in that tree.

Link: https://leetcode.com/problems/longest-zigzag-path-in-a-binary-tree/description/

Problem Explanation with examples:-

Example 1

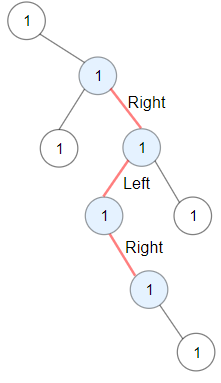
Input: root = [1,null,1,1,1,null,null,1,1,null,1,null,null,null,1,null,1]
Output: 3
Explanation: Longest ZigZag path in blue nodes (right -> left -> right).

Example 2

Input: root = [1,1,1,null,1,null,null,1,1,null,1]
Output: 4
Explanation: Longest ZigZag path in blue nodes (left -> right -> left -> right).

Example 3

Input: root = [1]
Output: 0

Constraints

The number of nodes in the tree is in the range [1, 5 * 104].
1 <= Node.val <= 100

Intuition:-

The longest zigzag path can be found by traversing the tree in a depth-first manner and keeping track of the longest zigzag path seen so far.
A stack is used to keep track of the nodes in the tree and the number of zigzags seen so far.
The stack is initialized with the root node and the number of zigzags seen so far is 0.
The stack is popped until it is empty. At each iteration, the current node, the number of zigzags seen so far, and a boolean left is popped from the stack.
If the current node is not None, the longest zigzag path seen so far is updated by comparing it with the number of zigzags seen so far.
The left child and the right child of the current node are pushed to the stack with the number of zigzags seen so far as 1 if left is True and n + 1 if left is False.
The longest zigzag path seen so far is returned.

Solution:-

Initialize ans to 0.
Initialize a stack and push the root node and the number of zigzags seen so far as 0 to the stack.
While the stack is not empty, pop the current node, the number of zigzags seen so far and a boolean left from the stack.
If the current node is not None, update ans by maximum of ans and n.
Push the left child of the current node to the stack with the number of zigzags seen so far as 1 if left is True and n + 1 if left is False. The boolean left is set to True.
Push the right child of the current node to the stack with the number of zigzags seen so far as n + 1 if left is True and 1 if left is False. The boolean left is set to False.
Return ans.

Code:-

JAVA Solution

class Solution {
    public String mergeAlternately(String word1, String word2) {
        int i = 0;
        int j = 0;
        StringBuilder ans = new StringBuilder();
        while (i < word1.length() && j < word2.length()) {
            ans.append(word1.charAt(i)).append(word2.charAt(j));
            i++;
            j++;
        }

        while (i < word1.length()) {
            ans.append(word1.charAt(i));
            i++;
        }

        while (j < word2.length()) {
            ans.append(word2.charAt(j));
            j++;
        }

        return ans.toString();
    }
}

Python Solution

class Solution:
    def longestZigZag(self, root: Optional[TreeNode]) -> int:
        ans = 0
        stack = [(root, 0, None)]
        while stack:
            node, n, left = stack.pop()
            if node:
                ans = max(ans, n)
                stack.append((node.left, 1 if left else n + 1, 1))
                stack.append((node.right, n + 1 if left else 1, 0))
        return ans

Complexity Analysis:-

TIME:-

The time complexity of the given Python code is O(N) where N is the number of nodes in the tree, as we visit every node exactly once.

SPACE:-

The space complexity of the code is also O(N) as we need to store all the nodes in the worst case (i.e., a skewed tree).

References:-

DFS in Binary Tree

Connect with me:-

java

python

leetcode

dsa