Spiral Matrix

Leetcode Daily Challenge (9th May, 2023)

9 May, 2023

Contributors

Lakshit Chiranjiv Sagar

@lakshit-cs

Problem Statement:-

Given an m x n matrix, return all elements of the matrix in spiral order.

Link: https://leetcode.com/problems/spiral-matrix/description/

Problem Explanation with examples:-

Example 1

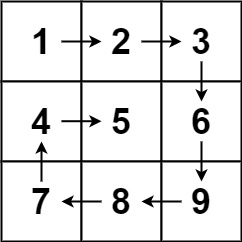
Input: matrix = [[1,2,3],[4,5,6],[7,8,9]]
Output: [1,2,3,6,9,8,7,4,5]

Example 2

Input: matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
Output: [1,2,3,4,8,12,11,10,9,5,6,7]

Constraints

m == matrix.length
n == matrix[i].length
1 <= m, n <= 10
-100 <= matrix[i][j] <= 100

Intuition:-

We can use a hashset to keep track of the visited indices and a variable order to keep track of the direction in which we are moving.
We can use a dfs approach to traverse the matrix in a spiral order and add the elements to the result list.
Recursively call the dfs function with the current indices and the current order and add the element at the current indices to the result list.

Solution:-

Initialize a variable res to an empty list.
If the matrix is empty, return res.
Initialize two variables m and n to the number of rows and columns in the matrix respectively.
Initialize a hashset to keep track of the visited indices.
Define a dfs function that takes the current indices and the current order as parameters.
If the current indices are out of bounds or the current indices are already visited, return.
Add the element at the current indices to the result list res and add the current indices to the hashset.
Define a list dirs that contains the directions in which we can move from the current indices.
Initialize a variable k to the current order.
While k is less than 4, recursively call the dfs function with the indices pointed by the kth element of dirs and k as parameters and increment k by 1 in each iteration.
Initialize k to 0.
While k is less than the current order, recursively call the dfs function with the indices pointed by the kth element of dirs and k as parameters and increment k by 1 in each iteration. This is done to cover the case when we are moving in the same direction as the previous iteration.
Call the dfs function with the indices (0,0) and 0 as parameters.
Return res.

Code:-

JAVA Solution

class Solution {
    public List<Integer> spiralOrder(int[][] matrix) {
        List<Integer> res = new ArrayList<>();
        if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
            return res;
        }
        int m = matrix.length, n = matrix[0].length;
        Set<String> visited = new HashSet<>();
        
        dfs(0, 0, 0);
        return res;
        
        void dfs(int i, int j, int order) {
            if (i < 0 || i >= m || j < 0 || j >= n || visited.contains(i + "," + j)) {
                return;
            }
            res.add(matrix[i][j]);
            visited.add(i + "," + j);
            int[][] dirs = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
            int k = order;
            while (k < 4) {
                int ni = i + dirs[k][0], nj = j + dirs[k][1];
                dfs(ni, nj, k);
                k++;
            }
            k = 0;
            while (k < order) {
                int ni = i + dirs[k][0], nj = j + dirs[k][1];
                dfs(ni, nj, k);
                k++;
            }
        }
    }
}

Python Solution

class Solution:
    def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
        res = []
        if not matrix:
            return res
        m, n = len(matrix), len(matrix[0])
        hashset = set()
        
        def dfs(i, j, order):
            if i < 0 or i >= m or j < 0 or j >= n or (i,j) in hashset:
                return
            res.append(matrix[i][j])
            hashset.add((i, j))
            dirs = [[i, j+1], [i+1, j], [i, j-1], [i-1, j]]
            k = order
            while k < 4:
                dfs(dirs[k][0], dirs[k][1], k)
                k += 1
            k = 0
            while k < order:
                dfs(dirs[k][0], dirs[k][1], k)
                k += 1
        
        dfs(0, 0, 0)
        return res

Complexity Analysis:-

TIME:-

The time complexity is O(mn), where m and n are the dimensions of the matrix, since it visits every cell exactly once.

SPACE:-

The space complexity is O(mn) since the HashSet can store at most m * n distinct cell positions.

References:-

Recursion

Connect with me:-

java

python

leetcode

dsa